The set theory is very important in order to understand data and databases. While you could live without it and still be a good SQL developer, understanding it will surely help a lot. So, let’s dive into the matter.
Set Theory – Math & Logic
I guess you remember these lessons from high school. To me, this was one of the most boring parts of my education, because many things sounded so obvious and you just had new notation and operators to work with sets – again pretty obvious one. While most people won’t use that knowledge later in their life, that’s not the case for those who are into databases.
What are Sets in the Set Theory?
Sets can contain really anything. Let’s start from the simplest possible set and that is the empty set – S = {}. As you can see, the empty set doesn’t contain any data. We don’t know anything about that set since it’s undefined – there are no data types or data values.
We could have a set of numbers S = {1, 2, 3}, or T = {1, 1, 2, 3, 1001}, or U = {3, 1, 2}. This is much more interesting, because we have values defined, and we can also tell that all of these sets contain numerical data.
Note. Two sets are equal if they contain same element, no matter how they are ordered. In our example, sets S = {1, 2, 3} & U = {3, 1, 2}, are the same.
Sets could also contain strings, e.g. A = {“Jack”, “Jill”, “John”}, B = {“Zagreb”, “Belgrade”, “New York”, “Berlin”, “Moscow”}.
Note: In the set theory, a set can contain anything, and the set elements even don’t have to be of the same type.
This is also a set: C = {1, “Jack”, 3.14, 2020/02/14}. It contains 4 separate information, and in this case, they have different data types.
We’re more interested in sets that contain structures/records/tuples. Let’s take a look at one such example country = {(1, Deutschland, Germany, DEU), (2, Srbija, Serbia, SRB), (3, Hrvatska, Croatia, HRV), (4, United States of America, United States of America, USA), (5, Polska, Poland, POL), (6, España, Spain, ESP), (7, Rossiya, Russia, RUS)}. We have a list of 7 structures containing data for 7 different countries. This is something we’ve already met, and these data are actually the contents of the country table from our model.
The Model
Let’s remind ourselves of the model we’re using in this article series.
If we’re talking from the perspective of the set theory, you can look at each table as one set. Same stands for query results. Technically the result of each query is a new table and you’ll treat it in the same manner as the regular table – this query result is also a set; you can write new queries using this query as a table etc.
Set Theory and Venn Diagrams
In SQL Server we have 3 important operators at our disposal – UNION (ALL), INTERSECT, and EXCEPT. They return the result of related operators from the set theory (on the picture below).
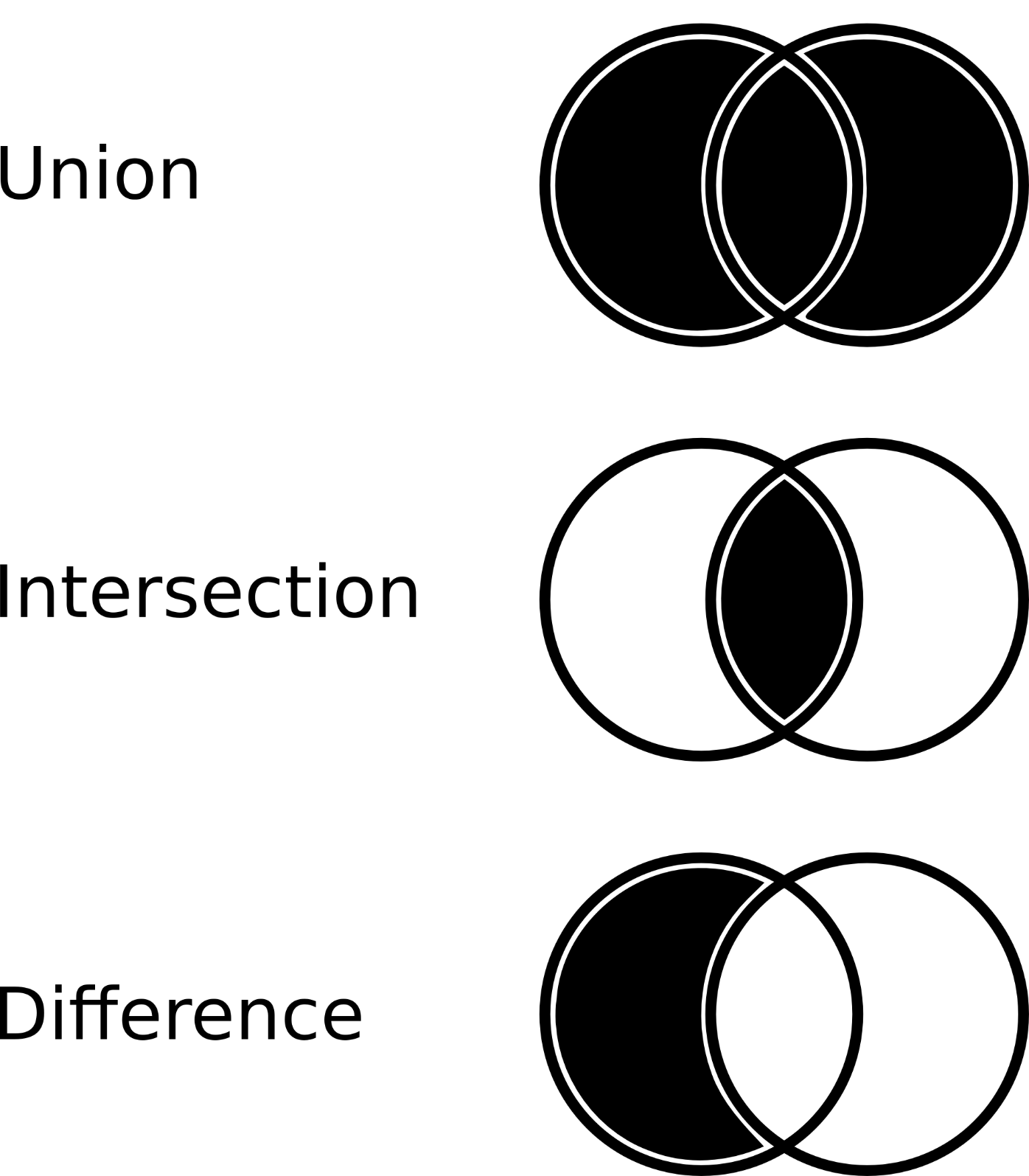
The easiest way to explain this is:
- UNION – Returns elements from both sets (if there are duplicates, they are in the final set, only once)
- UNION ALL – Same as the UNION operator, but will contain all duplicates
- INTERSECT – Returns a set containing elements that are present in both sets
- EXCEPT/MINUS (difference) – A MINUS B is a set containing elements from the set A that are not elements of the set B (so A MINUS (A INTERSECT B))
We won’t analyze situations where sets don’t have any common elements (A UNION B = all elements from A and B, A INTERSECT B = {}, A EXCEPT B = A, B EXCEPT A = B) and where set A = set B (A UNION B = A = B, A INTRSECT B = A = B, A EXCEPT B = B EXCEPT A = {}).
Set Theory and SQL
We talked a lot about the set theory so far, and now it’s time for some practice. We’ll write down a few queries which will show how UNION (ALL), INTERSECT and EXCEPT operators work.
#1 First we’ll test two separate queries and analyze the result set they return
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
-- list all customers with exactly 3 calls select customer.* from customer where id in ( select customer.id from customer inner join call on customer.id = call.customer_id group by customer.id having count(*) = 3 ); -- list all customers from Berlin select customer.* from customer inner join city on customer.city_id = city.id where city.city_name = 'Berlin'; |
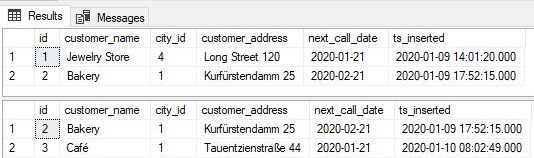
You should notice a few things:
- The first query returns all customers having exactly 3 calls
- The second query returns all customers from Berlin
- Both queries return the same columns, but rows returned are not the same. This is important because you can use operators working with sets only if these two sets are composed of elements with the same structure
- Each result set has 2 rows. “Bakery” is present in both result sets, and each set has one other row
#2 UNION and UNION ALL
Now we’ll use two available UNION operators. Any of these operators (UNION (ALL), INTERSECT, EXCEPT) is used in a way you just place it between queries.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
-- UNION -- list all customers with exactly 3 calls select customer.* from customer where id in ( select customer.id from customer inner join call on customer.id = call.customer_id group by customer.id having count(*) = 3 ) UNION -- list all customers from Berlin select customer.* from customer inner join city on customer.city_id = city.id where city.city_name = 'Berlin'; -- UNION ALL -- list all customers with exactly 3 calls select customer.* from customer where id in ( select customer.id from customer inner join call on customer.id = call.customer_id group by customer.id having count(*) = 3 ) UNION ALL -- list all customers from Berlin select customer.* from customer inner join city on customer.city_id = city.id where city.city_name = 'Berlin'; |
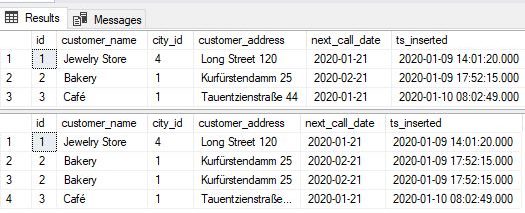
For these two result sets returned, you should notice the following:
- Each query, the first one using UNION, and the second one using UNION ALL returns 1 result set
- The result set returned by the UNION query returned all rows returned by the two queries used. The only difference is that the duplicated row had been eliminated
- The query using UNION ALL returned all rows from both queries, without removing duplicates
- The UNION is used more often, and you’ll probably use it when you have a few complex queries and you simply want to “join” their results without writing a single more complex query
#3 INTERSECT
The INTERSECT should return elements/rows which appear in both sets.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
-- INTERSECT -- list all customers with exactly 3 calls select customer.* from customer where id in ( select customer.id from customer inner join call on customer.id = call.customer_id group by customer.id having count(*) = 3 ) INTERSECT -- list all customers from Berlin select customer.* from customer inner join city on customer.city_id = city.id where city.city_name = 'Berlin'; |
Everything went as expected and you can see that the “Bakery” row was returned as a result.
#4 EXCEPT
The EXCEPT operator returns all elements/rows from the first set, except those that are in the second set.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
-- A EXCEPT B -- list all customers with exactly 3 calls select customer.* from customer where id in ( select customer.id from customer inner join call on customer.id = call.customer_id group by customer.id having count(*) = 3 ) EXCEPT -- list all customers from Berlin select customer.* from customer inner join city on customer.city_id = city.id where city.city_name = 'Berlin'; -- B EXCEPT A -- list all customers from Berlin select customer.* from customer inner join city on customer.city_id = city.id where city.city_name = 'Berlin' EXCEPT -- list all customers with exactly 3 calls select customer.* from customer where id in ( select customer.id from customer inner join call on customer.id = call.customer_id group by customer.id having count(*) = 3 ); |
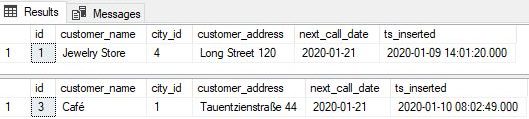
The most important thing you should notice here is:
- A EXCEPT B is not the same as B EXCEPT A (A and B are names of the sets)
- The first query returns all customers having exactly 3 calls except those from Berlin, while the second query finds and returns customers from Berlin except those with exactly 3 calls
Why Should You Understand the Set Theory?
Theory in IT is not so “hot” as the practice is. Same stands for the set theory. Still, understanding what lies in the background of the operations you run is essential for better understanding not only these operators but databases themselves.
Table of contents
His past and present engagements vary from database design and coding to teaching, consulting, and writing about databases. Also not to forget, BI, creating algorithms, chess, philately, 2 dogs, 2 cats, 1 wife, 1 baby...
You can find him on LinkedIn
View all posts by Emil Drkusic
- Learn SQL: How to prevent SQL Injection attacks - May 17, 2021
- Learn SQL: Dynamic SQL - March 3, 2021
- Learn SQL: SQL Injection - November 2, 2020