In this post we continue looking at the Cardinality Estimator (CE). The article explores some join estimation algorithms in the details, however this is not a comprehensive join estimation analysis, the goal of this article is to give a reader a flavor of join estimation in SQL Server.
The complexity of the CE process is that it should predict the result without any execution (at least in the current versions), in other words it should somehow model the real execution and based on that modeling get the number of rows. Depending on the chosen model the predicted result may be closer to the real one or not. One model may give very good results in one type of situations, but will fail in the other, the second one may fail the first set and succeed in the second one. That is why SQL server uses different approaches when estimating different types of operations with different properties. Joins are no exception to this.
The Demos
If you wish to follow this post executing scripts or test it yourself, below is the description of what we are using here. We use DB AdventureworksDW2016CTP3 and we use COMPATIBILITY_LEVEL setting to test SQL Server 2014 behavior (CE 120) and SQL Server 2016 behavior (CE 130).
For the demonstration purposes, we use two not officially documented, but well documented over the internet, trace flags (TFs):
- 3604 – Directs SQL Server output to console (Message window in SQL Server Management Studio (SSMS))
- 2363 – Starting from SQL Server 2014 outputs information about the estimation process
We are talking about estimations and we don’t actually need to execute the query, so don’t press “Execute” in SSMS otherwise a server will cache the query plan and we don’t need this. To compile a query and not to cache it, just press “Display Estimated Execution Plan” icon or press CTRL + L in SSMS.
Finally, we will switch to the AdventureworksDW2016CTP3 DB and clear server cache, I assume all the code below is located on the test server only.
|
1 2 3 |
use AdventureworksDW2016CTP3; dbcc freeproccache; go |
Join Estimation Strategies in SQL Server
During databases evolution (about half a century now) there were a lot of approaches how to estimate a JOIN, described in numerous research papers. Each DB vendor makes its own twists and improvements to classical algorithms or develops its own. In case of SQL Server these algorithms are proprietary and not public, so we can’t know all the details, however general things are documented. With that knowledge, and some patience, we can figure out some interesting things about the join estimation process.
If you recall my blog post about CE 2014 you may remember that the estimation process in the new framework is done with the help of such things as calculators – algorithms encapsulated into the classes and methods, the particular one is chosen for the estimation depending on the situation.
In this post we will look at two different join estimation strategies:
- Histogram Join
- Simple Join
Histogram Join
Let’s switch to CE 120 (SQL Server 2014) using a compatibility level and consider the following query.
Execute:
|
1 |
alter database [AdventureworksDW2016CTP3] set compatibility_level = 120; |
Display Estimated Execution Plan:
|
1 2 3 4 5 6 |
select * from dbo.FactInternetSales fis join dbo.DimDate dc on fis.ShipDateKey = dc.DateKey option(querytraceon 3604, querytraceon 2363); |
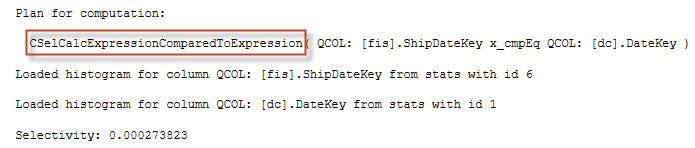
SQL Server uses this calculator in many other cases, and this output is not very informative in the meaning of how the JOIN is estimated. In fact, SQL Server has at least two options:
- Coarse Histogram Estimation
- Step-by-step Histogram Estimation
The first one is used in the new CE in SQL Server 2014 and 2016 by default. The second one is used by the earlier CE mechanism.
Step-by-step Histogram Estimation in the earlier versions used histogram alignment with step linear interpolation. The description of the general algorithm is beyond the scope of this article, however, if you are interested, I’ll refer you to the Nicolas’s Bruno (Software Developer, Microsoft) work “Statistics on Query Expressions in Relational Database Management Systems” COLUMBIA UNIVERSITY, 2003. And to give you the flavor of what’s going on, I’ll post an image from this work here:
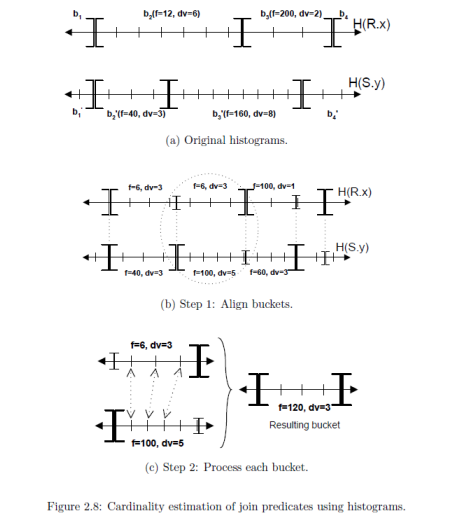
This is a general algorithm that gives an idea about how it works. As I have already mentioned, real algorithms are proprietary and not publicly available.
Coarse Histogram Estimation is a new algorithm and less documented, even in terms of general concepts. It is known that instead of aligning histograms step by step, it aligns them with only minimum and maximum histogram boundaries. This method potentially introduces less CE mistakes (not always however, because we remember that this is just a model). Now we will observe how it looks like inside SQL Server, for that purpose, we need to attach WinDbg with public symbols for SQL Server 2016 RTM.
Coarse alignment is the default algorithm under compatibility level higher than 110, and what we see in WinDbg in SQL Server 2016 is:
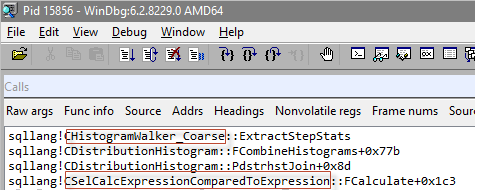
The breakpoint on the method CHistogramWalker_Coarse::ExtractStepStats is reached twice while optimizing the query above, because we have two histograms that are used for a join estimation and each of them are aligned in the coarse manner described above.
To take a step further, I also put a break point on the method CHistogramWalker_Coarse::FAdvance, which is also invoked twice, but before the ExtractStepStats, doing some preparation work. I stepped through it and examined some processor registers.
ASM command MOVSD moves the value 401412c160000000 from memory to the register xmm5 for some further manipulations. If you are wondering what is so special about this value, you may use hex to double calculator to convert this to double (I’m using this one):

Now let’s ask DBCC STATISTICS for the histogram statistics for the table’s FactInternetSales join column, in my case this statistic is named _WA_Sys_00000004_276EDEB3.
|
1 |
dbcc show_statistics(FactInternetSales, _WA_Sys_00000004_276EDEB3) with histogram; |
The result is:
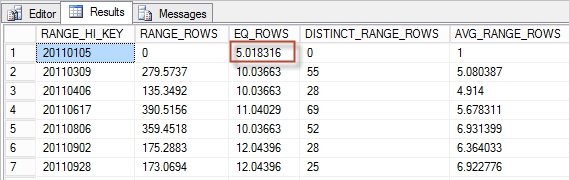
Look at the very first histogram row of the column that contains rows equal to the histogram upper boundary. This is the exact rounded value that was loaded by the method CHistogramWalker_Coarse::FAdvance before step estimation. If you spend more time in WInDbg you may figure out what exactly values are loaded then and what happens to them, but that is not the subject of this article and in my opinion is not so important. More important is the knowledge that there is a new default join histogram estimation algorithm that uses the minimum and maximum boundaries and it really works in this fashion.
Finally, let’s enable an actual execution plan to see the difference between actual rows and estimated rows, and run the query under different compatibility levels.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
alter database [AdventureworksDW2016CTP3] set compatibility_level = 110; go select * from dbo.FactInternetSales fis join dbo.DimDate dc on fis.ShipDateKey = dc.DateKey; go alter database [AdventureworksDW2016CTP3] set compatibility_level = 120; go select * from dbo.FactInternetSales fis join dbo.DimDate dc on fis.ShipDateKey = dc.DateKey; go alter database [AdventureworksDW2016CTP3] set compatibility_level = 130; go select * from dbo.FactInternetSales fis join dbo.DimDate dc on fis.ShipDateKey = dc.DateKey; go |
The results are:
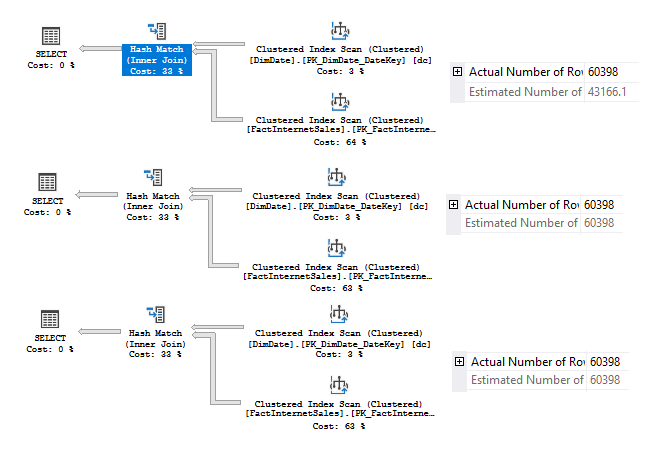
As we can see both CE 120 (SQL Server 2014) and CE 130 (SQL Server 2016) use Coarse Alignment and it is an absolute winner in this round. The old CE underestimates about 30% of the rows.
There are two model variations that may be enabled by TFs and affects the histogram alignment algorithm by changing the way the histogram is walked. Both of them are available in SQL Server 2014 and 2016, and produce different estimates, however, there is no information about what they are doing, and it is senseless to give an example here. I’ll update this paragraph if I get any information on that (If you wish you may drop me a line and I’ll send you those TFs).
Simple Join
In the previous section we talked about a situation when SQL Server uses histograms for the join estimation, however, that is not always possible. There is a number of situations, for example, join on multiple columns or join on mismatching type columns, where SQL Server cannot use a histogram.
In that case SQL Server uses Simple Join estimation algorithm. According to the document “Testing Cardinality Estimation Models in SQL Server” by Campbell Fraser et al., Microsoft Corporation simple join estimates in this way:

Before we start looking at the examples, I’d like to mention once again, that this is not a complete description of the join estimation behavior. The exact algorithms are proprietary and not available publicly. They are more complex and covers many edge cases which is hard to imagine in simple synthetic tests. That means that in a real world there might be the cases where the approaches described below will not work, however the goal of this article is not exploring algorithms internals, but rather giving an overview of how the estimations could be done in that or another scenario. Keeping that in mind, we’ll move on to the examples.
Simple join is implemented by three calculators in SQL Server:
- CSelCalcSimpleJoinWithDistinctCounts
- CSelCalcSimpleJoin
- CSelCalcSimpleJoinWithUpperBound (new in SQL Server 2016)
We will now look how does they work starting from the first one. Let’s, again, switch to CE 120 (SQL Server 2014) using compatibility level. Execute:
|
1 |
alter database [AdventureworksDW2016CTP3] set compatibility_level = 120; |
CSelCalcSimpleJoinWithDistinctCounts on Unique Keys
Press “Display Estimated Execution Plan” to compile the following query:
|
1 2 3 4 5 6 7 |
select * from dbo.FactInternetSales s join dbo.FactResellerSalesXL_CCI sr on s.SalesOrderNumber = sr.SalesOrderNumber and s.SalesOrderLineNumber = sr.SalesOrderLineNumber option (querytraceon 3604, querytraceon 2363) |
Table FactInternetSales has cardinality 60398 rows, table FactResellerSalesXL_CCI has cardinality 11669600 rows. Both tables have composite primary keys on (SalesOrderNumber, SalesOrderNumber). The query joins two tables on their primary keys (SalesOrderNumber, SalesOrderNumber).
In that case we have two columns equality predicate, and SQL Server can’t combine histogram steps because there are no multi-column histograms in SQL Server. Instead, it uses Simple Join on Distinct Count algorithm.
Let’s switch to the message tab in SSMS and observe the estimation process output. The interesting part is a plan for selectivity computation.
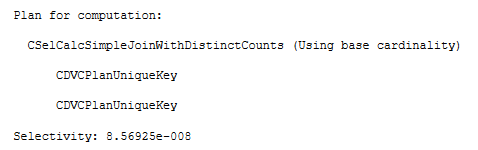
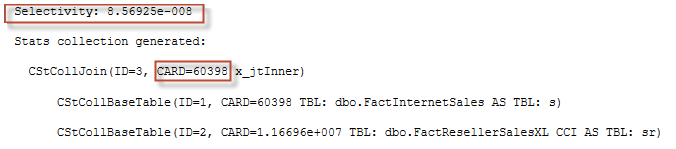
Parent calculator is CSelCalcSimpleJoinWithDistinctCounts that will use base table cardinality as an input (you may refer to my older blog post Join Containment Assumption and CE Model Variation to know the difference between base and input cardinality, however in this case we have no filters and it doesn’t really matter). As an input selectivity it will take two results from CDVCPlanUniqueKey sub-calculators. CDVC is an abbreviation for Class Distinct Values Calculator. This calculator will simply take the density of the unique key from the base statistics. We do have a multi-column statistics density because we have a composite primary key and auto-created multi-column stats. Let’s take a look at these densities:
|
1 2 |
dbcc show_statistics (FactInternetSales, PK_FactInternetSales_SalesOrderNumber_SalesOrderLineNumber) with density_vector; dbcc show_statistics (FactResellerSalesXL_CCI, PK_FactResellerSalesXL_CCI_SalesOrderNumber_SalesOrderLineNumber) with density_vector; |
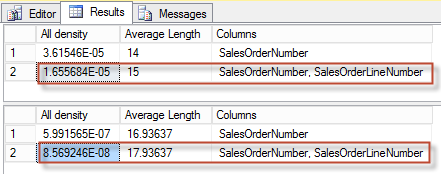
Now, the minimum of the two densities is taken as a join predicate selectivity. To get the join cardinality, we simply multiply two base table cardinalities and a join predicate selectivity (i.e. minimum density).
|
1 |
select 60398. * 11669600. * 8.569246E-08 -- 60397.802571984 |
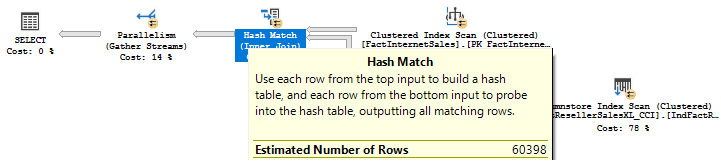
We got an estimate of 60397.8 rows or if we round it up 60398 rows. Let’s check with the TF output and with the query plan.
And the query plan:
CSelCalcSimpleJoinWithDistinctCounts on Unique Key and Multicolumn Statistics
The more interesting case is when SQL Server uses multicolumn statistics for the estimation, but there is no unique constraint. To look at this example, let’s compile the query similar to the previous one, but join FactInternetSales with the table FactInternetSalesReason. The table FactInternetSalesReason has a primary key on three columns (SalesOrderNumber, SalesOrderLineNumber, SalesReasonKey), so it also has multi-column statistics, but the combination (SalesOrderNumber, SalesOrderLineNumber) is not unique in that table.
|
1 2 3 4 5 6 7 |
select * from dbo.FactInternetSales s join dbo.FactInternetSalesReason sr on s.SalesOrderNumber = sr.SalesOrderNumber and s.SalesOrderLineNumber = sr.SalesOrderLineNumber option (querytraceon 3604, querytraceon 2363) |
Let’s look at the selectivity computation plan:
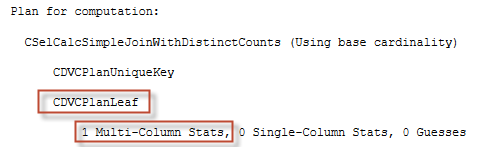
Parent calculator is still the same Simple Join On Distinct Counts, one sub-calculator is also the same, but the second sub-calculator is different, it is CDVCPlanLeaf with one multi-column stats available.
We’ll get the density from the first table and the second table multi-column statistics for the join column combination:
|
1 2 |
dbcc show_statistics (FactInternetSales, PK_FactInternetSales_SalesOrderNumber_SalesOrderLineNumber) with density_vector; dbcc show_statistics (FactInternetSalesReason, PK_FactInternetSalesReason_SalesOrderNumber_SalesOrderLineNumber_SalesReasonKey) with density_vector; |
And get the minimum of two:
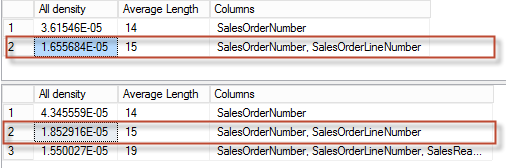
This time it will be the density from FactInternetSales – 1.655684E-05. This is picked as a join predicate selectivity, and now multiply base cardinalities of those tables by this selectivity.
|
1 |
select 60398. * 64515. * 1.655684E-05 -- 64515.0014399748 |
Let’s check with the results from SQL Server.
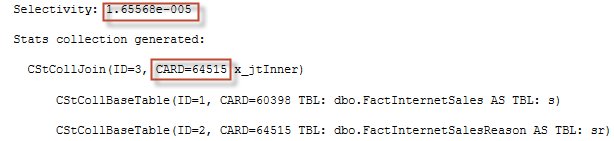
The query plan will show you also 64515 rows estimate in the join operator, however, I’ll omit the plan picture for brevity.
CSelCalcSimpleJoinWithDistinctCounts on Single Column Statistics
Finally let’s move on to the most common scenario, when there are no multi-column statistics, but there are single column statistics. Let’s compile the query (please don’t run this query, as it produces a huge result set):
|
1 2 3 4 5 6 7 |
select * from dbo.FactInternetSales si join dbo.FactResellerSales sr on si.CurrencyKey = sr.CurrencyKey and si.SalesTerritoryKey = sr.SalesTerritoryKey option (querytraceon 3604, querytraceon 2363) |
Again, we are joining FactInternetSales table, but this time with FactResellerSales table and on different columns: CurrencyKey and SalesTerritoryKey. Those columns have their own statistics and no multi-column stats. In that case SQL Server does more complicated mathematics, however, not too complex. In the SSMS message tab we may observe the plan for computation:
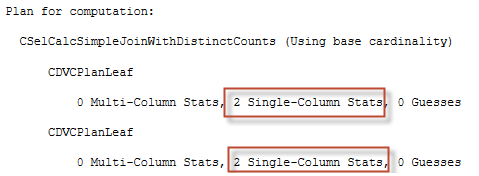
This time both sub-calculators are CDVCPlanLeaf and both of them are going to use 2 single-column statistics. SQL Server should somehow combine those statistics to get some common selectivity for the multi-column predicate. The next part of the output shows some computation details.
We’ll start with the first table FactInternetSales and the TF output related to it:
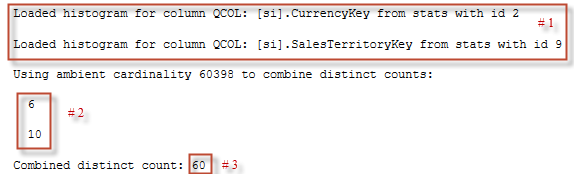
Two histograms (and in fact not only histograms, but the density vectors also) loaded for two columns, those statistics have ids 2 and 9 (# 1). Let’s query sys.stats to find them and look into.
|
1 2 3 |
select * from sys.stats where object_id = object_id('[dbo].[FactInternetSales]') and stats_id in (2,9) dbcc show_statistics (FactInternetSales, _WA_Sys_00000007_276EDEB3) with density_vector; dbcc show_statistics (FactInternetSales, _WA_Sys_00000008_276EDEB3) with density_vector; |
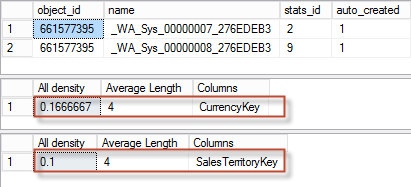
We see two densities for the two columns. The density is a measure of how many distinct values there are in the column, the formula is: density = 1/distinct_count. So to find distinct_count we use distinct_count = 1/density.
It will be:
|
1 2 |
select 1./0.1666667 -- 5.99999880 ~ 6 select 1./0.1 -- 10.000000 |
This is what we see in the computation output # 2.
Now SQL Server uses independency assumption, if we have 6 different CurrencyKeys and 10 different SalesTerritoryKeys, then how many unique pairs we may potentially have? It’s 6*10 = 60 unique pairs. So the combined distinct count is 60, as we can see in the output # 3.
The similar math is then done for the second table, I will omit the computation, just show the result.

So far we have: 60 distinct values for the first table and 50 distinct values for the second one. Now we’ll get the densities using the formula described above density = 1/distinct_count.
|
1 2 |
select 1E0/60. -- 0.0166666666666667 select 1E0/50. -- 0.02 |
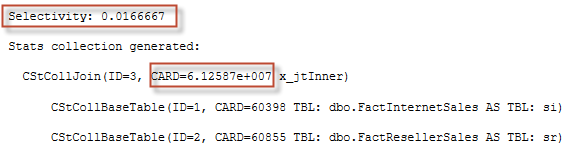
Again, like we have done before, pick the minimum one: 0.0166666666666667 or rounded up to 7 digits 0.1666667. This will be the join predicate selectivity.
Now get the join cardinality by multiplying it with table cardinalities:
|
1 |
select 0.0166666666666667 * 60398. * 60855. -- 61258671.5000001225173430 |
If we round up 61258671.5000001225173430 it will be 61258700.
Now let’s check with SQL Server.
And in the query plan:
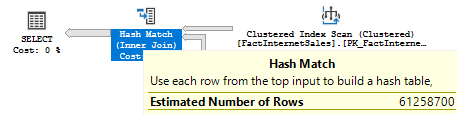
You see that the selectivity and rounded cardinality match with what we have calculated manually. Now move on to the next example.
CSelCalcSimpleJoin
It is possible to use distinct values when there is an equality predicate, because the distinct count tells us about how many unique discrete values are in the column and we may somehow combine the distinct count to model a join. If there is inequality predicate there is no more discrete values, we are talking about the intervals. In that case SQL Server uses calculator CSelCalcSimpleJoin.
The algorithm used for a simple join respects different cases, but we will stop at the simplest one. The empirical formula for this case is: join_predicate_selectivity = max(1/card1; 1/card2), where card1 and card2 is a cardinality of the joining tables.
To demonstrate the example, we will take the query from the previous part and replace equality comparison with an inequality.
|
1 2 3 4 5 6 7 |
select * from dbo.FactInternetSales s join dbo.FactResellerSalesXL_CCI sr on s.SalesOrderNumber = sr.SalesOrderNumber and s.SalesOrderLineNumber > sr.SalesOrderLineNumber option (querytraceon 3604, querytraceon 2363) |
The plan for computation on the message tab is:
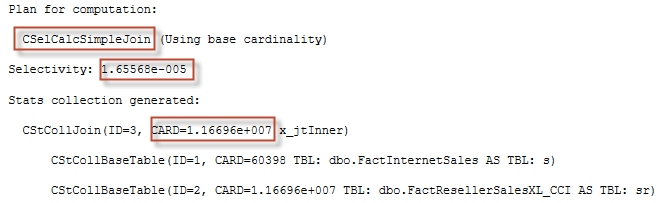
Not very informative, though you may notice a few interesting things.
First of all, the new calculator CSelCalcSimpleJoin is used instead of CSelCalcSimpleJoinOnDistinctCounts. The second is the selectivity, which is rounded maximum of: max(1/Cardinality of FactInternetSales; 1/Cardinality of FactResellerSalesXL_CCI).
|
1 |
select max(sel) from (values (1E+0/60398E+0), (1E+0/11669600E+0)) tbl(sel) -- 1.65568396304513E-05 ~ 1.65568E-05 |
The join cardinality is estimated as usual by multiplying base cardinalities with the join predicate selectivity, with obviously gives us 11669600:
|
1 |
select 1.65568396304513E-05 * 60398E+0 * 11669600E+0 – 11669600 |
We may observe this estimation in the query plan:
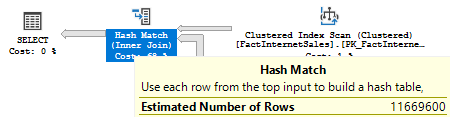
If the cardinality of the FactResellerSalesXL_CCI was less than cardinality of FactInternetSales, let’s say one row less 60398-1 = 60397, than the value 1/60397 would be picked. In that case the join cardinality would be 60398:
|
1 |
select (1E+0/60397E+0)* (60397E+0) * (60398E+0) -- 60398 |
Let’s test this by tricking the optimizer with update statistics command with undocumented argument rowcount like this:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
-- trick the optimizer update statistics FactResellerSalesXL_CCI with rowcount = 60397; go -- compile set showplan_xml on; go select * from dbo.FactInternetSales s join dbo.FactResellerSalesXL_CCI sr on s.SalesOrderNumber = sr.SalesOrderNumber and s.SalesOrderLineNumber > sr.SalesOrderLineNumber option (querytraceon 3604, querytraceon 2363) go set showplan_xml off; go -- return to original row count update statistics FactResellerSalesXL_CCI with rowcount = 11669600; |
If you switch to the message tab you will see that the join selectivity is now 1.65571e-005:
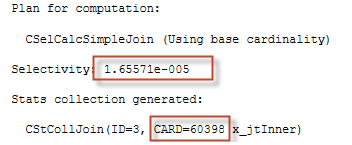
Which is rounded value of:
|
1 |
select 1E0/60397E0 -- 1.65571137639287E-05 |
And the join cardinality is now 60398, as well as in the query plan:
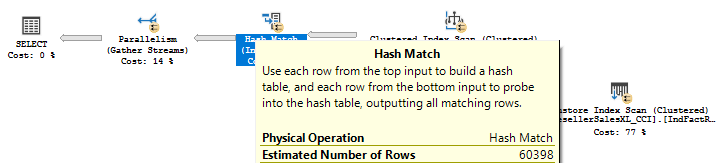
We’ll now move on to the next calculator, new in SQL Server 2016 and CE 130.
CSelCalcSimpleJoinWithUpperBound (new in 2016)
If we compile the last query under 120 compatibility level and 130 we will notice the estimation differences. I will add a TF 9453 to the second query, that restricts Batch execution mode and a misleading Bitmap Filter (misleading only in our demo purposes, as we need only join and no other operators). To be honest, we may add this TF to the first one query also, though it is not necessary. (Frankly speaking this TF is not needed at all, because it does not influence the estimate, however, I’d like to have a simple join plan for the demo).
Let’s run the script to observe the different estimates:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
alter database [AdventureworksDW2016CTP3] set compatibility_level = 120; go set showplan_xml on; go select * from dbo.FactInternetSales s join dbo.FactResellerSalesXL_CCI sr on s.SalesOrderNumber = sr.SalesOrderNumber and s.SalesOrderLineNumber > sr.SalesOrderLineNumber option (querytraceon 3604, querytraceon 2363, querytraceon 9453); go set showplan_xml off; go alter database [AdventureworksDW2016CTP3] set compatibility_level = 130; go set showplan_xml on; go select * from dbo.FactInternetSales s join dbo.FactResellerSalesXL_CCI sr on s.SalesOrderNumber = sr.SalesOrderNumber and s.SalesOrderLineNumber > sr.SalesOrderLineNumber option (querytraceon 3604, querytraceon 2363, querytraceon 9453); go set showplan_xml off; go |
The estimates are very different:
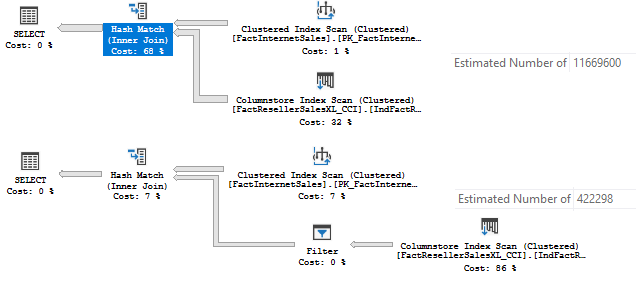
Eleven million rows for the CE 120 and half a million for CE 130.
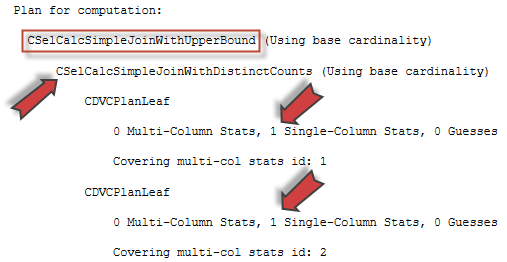
If we inspect the TF output for the CE 130, we will see that it doesn’t use calculator CSelCalcSimpleJoin, but uses the new one CSelCalcSimpleJoinWithUpperBound.
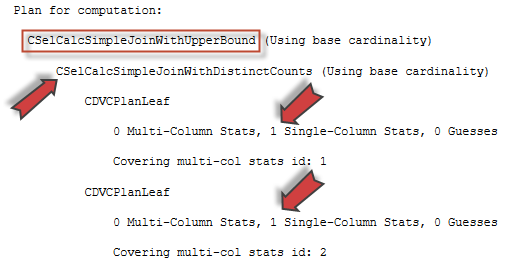
You may also note that as a sub-calculator it uses already familiar to us calculator CSelCalcSimpleJoinWithDistinctCounts, described earlier, and this sub-calculator uses single column statistics.
If we look further, we will see that the statistics is loaded for the equality part of the join predicate on columns SalesOrderNumber for both tables.
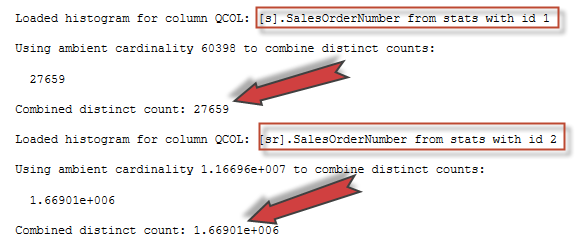
Combined distinct counts could be found from the density vectors as we saw earlier in this post:
|
1 2 |
dbcc show_statistics (FactInternetSales, PK_FactInternetSales_SalesOrderNumber_SalesOrderLineNumber) with density_vector; dbcc show_statistics (FactResellerSalesXL_CCI, PK_FactResellerSalesXL_CCI_SalesOrderNumber_SalesOrderLineNumber) with density_vector; |
So the distinct count would be:
|
1 2 |
select 1E0/3.61546E-05 -- 27658.9977485576 select 1E0/5.991565E-07 -- 1669013.02080508 |
Which equals to what we see in the output after round up. There is no need to combine distinct values here, because the equality part contains only one equality predicate (s.SalesOrderNumber = sr.SalesOrderNumber), but if we had condition like: join … on a1=a2 and b1=b2 and c1<c3, then we could combine distinct values for the part a1=a2 and b1=b2 to calculate its selectivity.
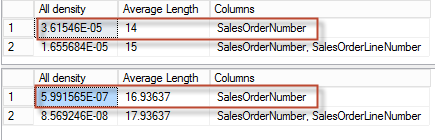
In this case we will simply take the minimum of densities – 5.99157e-007 and multiply cardinalities with it:
|
1 |
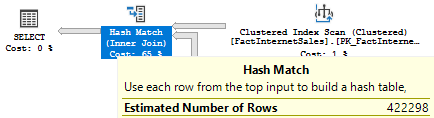
select 5.99157e-007 * 60398E0 * 11669600E0 -- 422298.136797826 |
This cardinality will be the upper boundary for the Simple Join estimation. If we look at the plan, we’ll see that this boundary is used as an estimate:
If we trick the optimizer with the script as we did before:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
-- trick the optimizer update statistics FactResellerSalesXL_CCI with rowcount = 60397; -- modified go -- compile set showplan_xml on; go select * from dbo.FactInternetSales s join dbo.FactResellerSalesXL_CCI sr on s.SalesOrderNumber = sr.SalesOrderNumber and s.SalesOrderLineNumber > sr.SalesOrderLineNumber option (querytraceon 3604, querytraceon 2363, querytraceon 9453, maxdop 1) go set showplan_xml off; go -- return to original row count update statistics FactResellerSalesXL_CCI with rowcount = 11669600; |
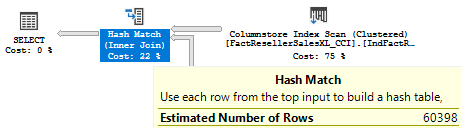
We won’t get the estimate:
|
1 |
select 5.99157e-007 * 60398E0 * 60397E0 -- 2185.63965930094 |
Because this time the upper boundary is less than a simple join estimate (demonstrated earlier), so the last one will be picked:
Finally I ran this query to get the actual number of rows:
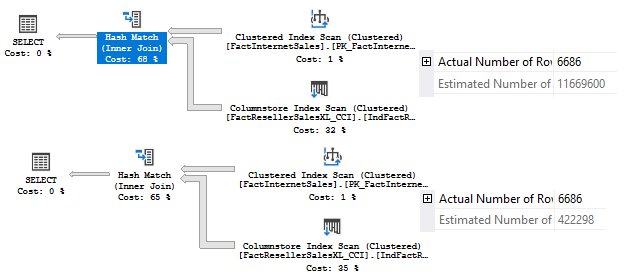
Both CE heavily overestimates. However, the 130 CE is closer to the truth.
Model Variation
There is a TF that forces the optimizer to use Simple Join algorithm even if a histogram is available. I will give you this one for the test and educational purposes. TF 9479 will force optimizer to use a simple join estimation algorithm, it may be CSelCalcSimpleJoinWithDistinctCounts, CSelCalcSimpleJoin or CSelCalcSimpleJoinWithUpperBound, depending on the compatibility level and predicate comparison type. You may use it for the test purposes and in the test enviroment only.
Summary
There is a lot of information about join estimation algorithms over the internet, but very few about how SQL Server does it. This article showed some cases and demonstrated its maths and internals in calculating joins cardinality. This is by no means a comprehensive join estimation analysis article, but a short insight into this world. There are much more join algorithms, even if we look at the calculators: CSelCalcAscendingKeyJoin, CSelCalcFixedJoin, CSelCalcIndependentJoin, CSelCalcNegativeJoin, CSelCalcGuessComparisonJoin. And if we remember that one calculator can encapsulate several algorithms and SQL Server can even combine calculators – that is a really huge field of variants.
I think you now have an idea how the join estimation is done and how subtle differences about predicate types, count, comparison operators influence the estimates.
Thank you for reading!
- SQL Server 2017: Adaptive Join Internals - April 30, 2018
- SQL Server 2017: How to Get a Parallel Plan - April 28, 2018
- SQL Server 2017: Statistics to Compile a Query Plan - April 28, 2018