With the introduction of Microsoft’s new In-Memory OLTP engine (code name Hekaton) the familiar B-Tree indexes were not always the optimal solution. The target of the Hekaton project was to achieve 100 (hundred) times faster OLTP processing, and to help this a new index was introduced – the hash index.
The hash index is ideal solution to optimize queries scanning the indexed columns in result of a WHERE clause on exact equality on the index key column(s).
|
1 2 3 4 |
SELECT LastName FROM EmpInformation WHERE LastName = Bell |
We will discuss the hash indexes, their internal structure (1), how they work with the standard data modification statements (2), and the important properties taken under consideration upon their creation (3).
Simply explained, in the In-Memory OLTP Engine, hash indexes are collection of buckets organized in an array. Each bucket contains a pointer to a data row.
To start, let us review how a row looks like when stored in an in-memory table. It consists of system data holding the row timestamp and the index pointer and the second part with the user data.
The timestamp contains a BeginTs timestamp showing us the “time” when a row was inserted (created) and an EndTs stamp showing the “time” when a row is no longer valid (deleted or updated). BeginTs and EndTs correspond to the Global Transaction Timestamp of the transaction that acted lastly on that row. In our case, the BeginTs is 10 and the EndTs is infinity – meaning that the row was inserted at time “10” and is valid until infinity or of course DML operations occurs.

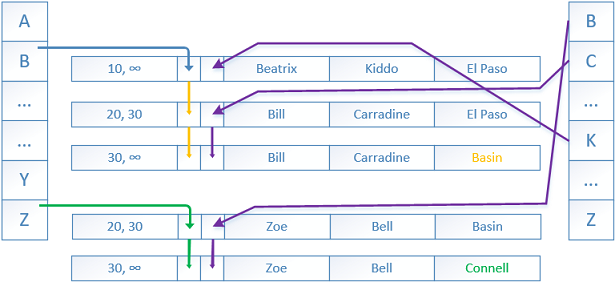
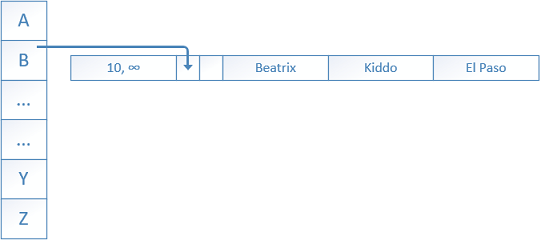
1. When a new row is inserted into the table a deterministic hash function maps the index key into the corresponding bucket within the hash index. In our case the hash index is on the column ‘FirstName’ and the value ‘Beatrix’ was put into hash bucket B (bucket is named ‘B’ this is for illustration purposes), a pointer is created linking the bucket and the row. The hash function is always deterministic which means that it provides the same hash result every time when given the same input – duplicate values will have the same hash value. The same hash function is used for each and every hash index. The result distribution is relatively random and on repeated calls, the outputs of the hash function tend to form a Poisson* or bell curve distribution, not a flat linear distribution. The hash function is similar to the HASHBYTES/CHECKSUM** T-SQL system functions.
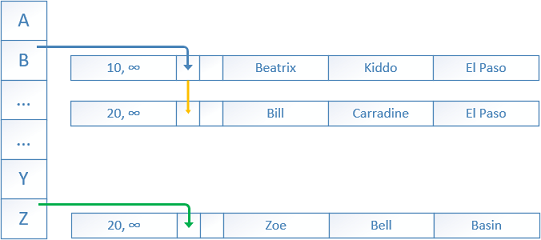
2. A little later two more rows are inserted by another transaction at the “time” BeginTs 20.
The first row has value ‘Bill’ that is placed again in the bucket ‘B’ by the hashing function.
A new pointer is created to that row from the previous one.
The second inserted row has a value ‘Zoe’ for ‘FirstName’ which is placed in the bucket ‘Z’ by the hashing function.
A new pointer is created to that row originating from the bucket.
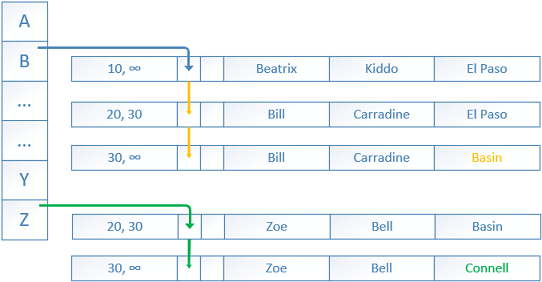
Next, an UPDATE transaction with BeginTs “time” of 30 needs to update two rows – Bill is moving to the city Basin, Zoe is moving to the city Connell.
The current rows are updated only with an EndTs value of 30 showing that the rows are not the most recent anymore.
New rows are added with BeginTs of 30 and EndTs of infinity. New pointers are created from the previous rows to the new ones.
The old rows will be eventually unlinked and then deleted by the garbage collector.
The DELETE statement acts in the same manner, of course with the difference that it updates the EndTs without adding a new row.
If a new SELECT session starts with a Global Transaction Timestamp higher than 30 the old rows (20->30) will not be visible to it.
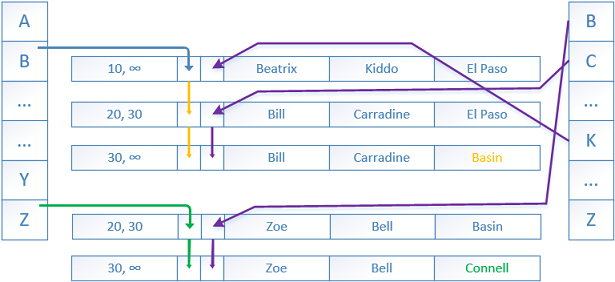
In-memory OLTP tables support more than one hash index, each of them with separate array of buckets and pointers.
Here, the secondary index is created on the second column ‘LastName’. The rows are linked with pointers in a different order, but still following the versioning.
Every memory optimized table should have at least one and up to eight indexes. A unique primary key should be defined as well, the primary key is counted as one of the eight-index limit and is not updatable.
(3) Hash indexes can be created as a part of the in-memory OLTP table creation or added later using the ALTER statement.
The most important parameter is the BUCKET_COUNT, for SQL Server 2016. It can subsequently be changed using the ALTER TABLE EmpInformation … ALTER INDEX REBUILD syntax.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
CREATE TABLE EmpInformation ( EmpID int NOT NULL IDENTITY(1,1) PRIMARY KEY NONCLUSTERED, FirstName nvarchar(25) NOT NULL, LastName nvarchar(25) NOT NULL, City nvarchar(25) NULL, INDEX IX_Hash_FirstName HASH (FirstName) WITH (BUCKET_COUNT = 100000) ) WITH ( MEMORY_OPTIMIZED = ON, DURABILITY = SCHEMA_AND_DATA); GO ALTER TABLE EmpInformation ADD INDEX IX_Hash_LastName HASH (LastName) WITH (BUCKET_COUNT = 80000); -- Setting BUCKET_COUNT 80000 will result in 131072 buckets (rounded by the SQL Server to next power of two) |
The number of buckets and the amount of data within the index directly affects performance. The buckets are an 8 byte object which stores a link pointer to the key entries of the rows. Each row that is part of an index is linked by one parent and is pointing to a single child, this is known as a chain.
If you are working with a high number of data rows and low number of buckets, the chains will be longer and scan operations will require numerous steps resulting in performance degradation. Note that scan operations are also required to locate the row in order to update the EndTs when UPDATE or DELETE statement is performed. And of course high number of buckets and low number of data rows affects negatively full table scans and of course reserves and waste memory.
There is no formula or golden ratio which should be followed when choosing the bucket count. It is recommended by Microsoft**** to have a BUCKET_COUNT between one and two times the number of distinct values in the index. Example is if you are having a table dbo.Orders with 100 000 distinct order IDs the bucket count should be between 100 000 and 200 000. Here it is most important to take under consideration the future growth due to the nature of the table.
Remember that hash indexes are not optimal when working with a column containing high number of duplicates. The duplicate values generate the same hash which results in a very long chains. Generally, if the ratio of all values versus the distinct ones is higher than 10 you should consider a range index instead.
An example is if you have 100 000 total employees in a table and the distinct job titles shared between them is 300, this leads to a ratio of ~333 (100 000 / 300), meaning you should consider range index instead. When considering the cardinality of the data, ratio of 10 and lower is considered optimal.
- Performance tuning for Azure SQL Databases - July 21, 2017
- Deep dive into SQL Server Extended events – The Event Pairing target - May 30, 2017
- Deep dive into the Extended Events – Histogram target - May 24, 2017