The Java HashCode method is used to determine uniqueness or similarity of strings. While implemented in Java, there can be many benefits of creating a similar or customized version of this method.

Introduction

Determine uniqueness or similarity between strings is often important, both in application code and in database scripts. While SQL Server has many built-in functions that can be used to generate hash values or checksums, there is sometimes the need to use a specific algorithm that is similar to one used in code.

This article mirrors a need that arose unexpectedly in which there was a desire to validate Java HashCode values for many elements in a list and manage those results within SQL Server. For the application being addressed, this would improve the efficiency of code by allowing set-based comparisons, rather than code pulling rows in batches (or one at a time).

We will build from scratch a TSQL version of HashCode, explaining each component, how it works, and supplying a handful of demos that show how to build and use it in any SQL Server environment.

Why Hash?

There are many different reasons why we would be interested in hashing data, regardless of whether we use HashCode, or some other algorithm.

The primary use of hashing is for the organization and location of data. Data can be mapped into a set of hash buckets, where we can control the number and size of those buckets. When we need to locate a value or set of values at a later time, we can reduce our search to only those with a similar hash.

Hashing is very effective at describing the similarity or differences between data values. Identical hashes indicate values that are identical or very similar, whereas differing hashes indicate values that are unique.

Hashing can also be used to verify if a data element was transmitted successfully across a network or between machines. While a checksum is very effective for this purpose, there can be benefits to customizing a hash specifically for a given application’s needs.

One other use of hashing is to index encrypted data (when needed). By taking a hash of an unencrypted value prior to encryption, we can create a column that can be indexed and searched when decryption is required. This allows us to greatly reduce the search space from a table scan to an index seek in which the resulting number of rows to read will be small.

Details of HashCode

The goal of any hash function is to map data into corresponding buckets in a target data type as evenly as possible. Mathematically, there are many ways to accomplish this, with most involving sums, products, powers, or division of each character of data involved. Prime numbers are often used in these calculations in order to ensure as much uniqueness as possible in each calculation.

Our ultimate goal is to return the hash of any string or set of strings that are passed into the HashCode method. The method itself is based on a mathematical formula that sums hashes for each character within a string:

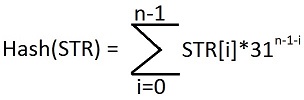
Where:
STR: The input string
n: Number of characters in the string
i: Current character in the string
31: An arbitrary prime number.

The arbitrary prime number helps ensure that we cover a field of numbers large enough to encompass strings of a given length. Larger strings warrant larger calculations. As a result, the size of the hash result, whether it can be SMALLINT, INT, BIGINT, or a DECIMAL calculation, can be determined by string complexity. For the sake of our demonstrations, we will use 31 as the prime number, and INT for the hash results, which is identical to the HashCode function as is currently implemented in Java.

For any application of this function to relatively small strings, this will be more than sufficient. If you were looking to run hashes against VARCHAR(MAX) columns, large volumes of strings, or some combination of those 2, then you might want to consider using DECIMAL to gain even more digits. It is unclear why we would want to hash the full text of large comments, descriptions, or text, but if the need exists, we can adjust our scripts to accommodate as needed.

An obvious question: What happens when our sums exceed the boundaries of the data type used for the results? In that scenario, the result is rolled up or down by half of the range of our data type. This preserves all bits within our hash, while removing the leading excess bit. We’ll run through a few examples below in order to see how this works.

If we want to calculate the HashCode for multiple strings, the result is the sum of HashCodes for all strings, calculated independently. As with the summations performed above, if we are summing multiple HashCode values and overflow our output data type, then we negate the result and remove the leading bit in order to “rollover” and continue summing effectively and predictably. Since each string is calculated separately, the order of distinct strings does not matter when determining HashCode values.

Uniqueness

An important note about hash functions in general is that they do not guarantee uniqueness! Two identical objects will generate the same hash every time it is calculated, but two unequal objects can have the same hash code. Similarly, two objects with the same hash might actually be different—though they are likely to be quite similar to each other.

The number of possible strings that exist with combinations of any characters will always be far greater than an INT, or a BIGINT for that matter. For most applications, HashCode will provide more than enough uniqueness and identification value to be worthwhile, but it is important to note that it does not guarantee uniqueness.

Within the scope a given application, duplication will typically be minimal, but it is worth noting that it is not mathematically impossible, nor is uniqueness guaranteed.

For example, consider the HashCode values for “Aa” vs. “BB”:
The following are the ASCII values for the characters above:
A: 65 a: 97 B: 66

Therefore, the calculations for these strings would be:
Aa = 65 * 31^2-1-0 + 97 * 31^2-1-1 = 2,015 + 97 = 2,112.
BB = 66 * 31^2-1-0 + 66 * 31^2-1-1 = 2,015 + 97 = 2,112.

As a result, very short strings are far more likely to result in duplication. Additionally, strings with a very limited variety of characters will also result in duplication more often. If you are using a hash algorithm similar to this in order to compare very short or non-diverse strings, consider also performing an equality check to validate the dummy scenario in which two strings are overly simplistic in nature. As a bonus, the comparison cost of two simple strings will be relatively inexpensive.

To sum up uniqueness:

• Two identical strings or sets of strings will result in the same HashCode.
• Multiple strings presented in different orders will produce the same HashCode.
• Two identical HashCodes can represent two different strings, although this is very, very unlikely.
• Two different strings can result in the same HashCode, although this is very, very unlikely.
• The more different strings that are analyzed, the greater the probability of a collision.

HashCode is excellent for comparing strings, but should never be used as a key for determining uniqueness with certainty, nor should it be used as a primary or alternate key on a table. Alternatively, HashCode can be used to determine if two different strings or set of strings are similar. If the hashes are identical, the values can be further analyzed as needed, whereas if they are different, we can move on with the knowledge that they are definitely not identical.

Example Hash Results

Our inputs for any tests we perform will be comma-delimited lists of strings. For these examples, the HashCode value is calculated for each item in the list, and then those values are added together. For example, consider the string “Table, Column, Function, Stored Procedure, Index”. This list contains 5 elements and will be broken down as follows:

HashCode(‘Table,Column,Function,Stored Procedure,Index’) =
HashCode(‘Table’) + HashCode(‘Column) + HashCode(‘Function) + HashCode(‘Stored Procedure) + HashCode(‘Index’) =
HashCode(‘Table’) = 84 * 31^5-1-0 + 97 * 31^5-1-1 + 98 * 31^5-1-2 + 108 * 31^5-1-3 + 101 * 31^5-1-4 = 80,563,118
HashCode(‘Column) = 67 * 316^6-1-0 + 111 * 316^6-1-1 + 108 * 31^6-1-2 + 117 * 31^6-1-3 + 109 * 31^6-1-4 + 110 * 31^6-1-5 = 2,023,997,302
HashCode(‘Function’) = 67 * 316^8-1-0 + 111 * 316^8-1-1 + 108 * 318^8-1-2 + 117 * 31^8-1-3 + 109 * 318^8-1-4 + 110 * 31^8-1-5 + 110 * 31^8-1-6 + 110 * 31^8-1-7 = 1,445,582,840
HashCode(‘Stored Procedure’) = 67 * 316^16-1-0 + 111 * 316^16-1-1 + 108 * 318^16-1-2 + 117 * 31^16-1-3 + 109 * 318^16-1-4 + 110 * 31^16-1-5 + 110 * 31^16-1-6 + 110 * 31^16-1-7 + 67 * 316^16-1-8 + 111 * 316^16-1-9 + 108 * 318^16-1-10 + 117 * 31^16-1-11 + 109 * 318^16-1-12 + 110 * 31^16–1-13 + 110 * 31^16–1-14 + 110 * 31^16–1-15 = -1,281,122,736
HashCode(‘Index’) = 73 * 31^5-1-0 + 110 * 31^5-1-1 + 100 * 31^5-1-2 + 101 * 31^5-1-3 + 120 * 31^5-1-4 = 70,793,394

HashCode(‘Table, Column, Function, Stored Procedure, Index’) = 2,339,813,918…
BUT, since this value is greater than the bounds of an INTEGER, we need to lop off the leading digit as follows:

HashCode(‘Table,Column,Function,Stored Procedure,Index’) = 2,339,813,918 – 2³² = -1,955,153,378.

This additional bit of arithmetic allows us to ensure that all results stay within the boundaries of the data type we have chosen (INT). If we used BIGINT instead, then we would need to take action on our results when they exceeded the bounds of -2⁶³ to 2⁶³– 1, at which point we would add or subtract 2⁶⁴ in order to maintain our results as valid BIGINT values.

Building HashCode in TSQL

The challenge at hand is to build a TSQL function that can do all of this for us, both accurately and quickly. To accomplish this, let’s break down the problem into a number of simpler, discrete steps, each of which we can table separately, and then put back together at the end in order to achieve our goals:

1. Create or use a method for parsing comma-delimited strings.
2. Create a function that accepts a single delimited list that will be parsed into discrete strings to be processed.
3. Loop through each string, one at a time, in order to calculate the HashCode value for each one separately. Within this loop, we will:
   1. Loop through each character in that string.
   2. Get the ASCII value for that character.
   3. Calculate the HashCode value for that ASCII code.
   4. Add to the running total for the HashCode for this string
   5. If the HashCode of this is greater than the boundaries of an INT, adjust back into those bounds.
   6. Add the result to the running total for all strings to be hashed.
   7. If the grand total is outside of the bounds of an INT, adjust in the same fashion as we did above.
4. Return the HashCode total from the function.

There are many ways to parse a delimited string. Feel free to reference a previous article in which this topic was delved into quite thoroughly:
Efficient creation and parsing of delimited strings

For simplicity—and for keeping our code simple, we will use the function STRING_SPLIT, which is included by default in all versions of SQL Server starting with 2016. Feel free to use any other string-splitting method at your disposal, whether it be in the article above, or an in-house solution that you use elsewhere in your database schema.

With that bit of housekeeping out of the way, we can declare our function:

You may ask, “Why does the function return a BIGINT, when the value should always be an INT? For our work below, I’ve chosen to use BIGINT for all numeric data types. This allows easy expansion of the result set into BIGINT instead of INT, with only a few changes to the underlying calculations. We need to use BIGINT in order to track running totals within the function, as they will often exceed the boundaries of an integer briefly, until adjusted at the end of each loop. Using BIGINT everywhere maintains consistency across all of our variables.

To begin our function, we’ll declare a variety of variables that will be used throughout our calculations, as well as perform our string splitting:

The @Input_Strings table will be used to store the set of strings passed into the function, which are parsed and inserted using STRING_SPLIT, or any other favorite list-splitting method. The remainder of the variables will be used for loop variables or as placeholders for details about string lengths or the prime number we are choosing (31). With this housekeeping out of the way, we will use a CURSOR to loop through each string. A WHILE loop could also be used, with similar results.

With a loop CURSOR defined, we can now iterate through each string and calculate the HashCode of each, one character at a time:

The check of @@FETCH_STATUS allows us to continue looping until the cursor returns no further items from a FETCH command. We then assign the length of the string to a variable and reset the character counter, which will loop until we hit the length of the string. @Java_Hashcode_Output will store the running total results for the current string, to be used when the inner loop is complete:

The WHILE loop will iterate once per character in the current string that is being examined. The @Current_Character pulls one character at a time as we run through this loop. We then proceed to determine the ASCII value of the character, also storing that in a scalar variable (@Current_Character_Ascii_Value).

Now we perform the important calculation of the HashCode for this character, which multiplies our existing output by our prime number (31) and adds it to the current character’s ASCII value. We then calculate the modulus (remainder) between that result and 2³². The modulus operation allows us to continue making our summation calculations accurately without rolling more than one power of 2 out of bounds of an INT. For longer strings, this is very important to prevent our calculations from becoming astronomically large!

With each loop, we continue to calculate the HashCode value using the existing value, as well as variables for the given character. Lastly, we increment @Character_Counter and continue until we are finished with the current string.

After each HashCode calculation, we need to validate that the results are within the range of our output data type, in this case, INTEGER. The following TSQL will validate and adjust, if needed:

The first IF statement checks to see if our HashCode output exceeds 2³¹, in which case we subtract 2³² from our result, moving it into negative territory, but not beyond the scope of an INTEGER. This effectively is removing the leading bit from the result and negating it.

The second IF statement checks for the opposite condition, where the HashCode output is less than -2³¹, in which case we add 2³² from our result, removing the leading bit from the negative number and negating it.

We have now calculated the HashCode for the first string in our sequence! If that was the only string supplied in the input list, then we are done, otherwise we will move to the start of the loop and perform our calculations on the next string. In order to keep a running total of HashCodes for each string, we will sum our result with a running total variable, @Java_Hashcode_Output_Total:

In the first loop, @Java_Hashcode_Output_Total will equal @Java_Hashcode_Output, but in future iterations will run the chance of exceeding the boundaries of an INTEGER. Our solution to this problem is exactly the same as how we dealt with this problem above:

These two calculations should look very familiar! They are almost identical to how we kept our HashCode result for a single string within the range of our output variable. If the running total for our entire string list exceeds the boundaries of an INTEGER, on the positive or negative side of the range, then we will add or subtract 2³² from the result to move it back within our acceptable result set.

With the string calculation, as well as a running total complete, we can fetch the next string from our cursor and continue with the next calculation:

This loop will continue until we have calculated the HashCode for every string, and added those results to the running total across all results. Once done, we can clean up the cursor, return our results, and be done with this function:

That’s it—all in about 75 lines of TSQL! The most frequently-made mistake when trying to convert a hashing algorithm into TSQL is handling overflow situations in which results exceed the boundaries of our output data type. In this script, we used the INTEGER data type to handle output results, allowing for 4,294,967,296 distinct possible result values. Integer was chosen to match the behavior of the HashCode method as written in Java, but could be altered to use a BIGINT instead, which would provide 18,446,744,073,709,551,616 values within the allowable range. While it may seem like crazy talk to write out numbers that large, but if uniqueness were more important, and we wanted a significantly larger result range with less chances for collisions, then the larger values would provide that additional buffer against duplication.

If, for any reason BIGINT was still inadequate, we could introduce a DECIMAL type, which allows results between -10³⁸+1 and 10³⁸-1. If uniqueness is so critical that numbers that absurdly large aren’t good enough, then hashing may not be the correct way to manage your data. It may instead be necessary to compare data as-is, or encrypt using a more complex algorithm that guarantees uniqueness. Hashing provides a high level of uniqueness using very inexpensive calculations, which are good enough for most common uses.

Example Function Use

Calling our HashCode function is as easy as including it in a SELECT statement:

The result is a single BIGINT (within the range of an integer):

376744202

As with any function, we can use the function as part of a result set when selecting data from a table. As always, test performance against any large data sets before moving into a production environment. Assuming it passes the speed test, you can accomplish this with a query similar to this:

These values could then be summed up, if desired, or other calculations performed on the results.

Conclusion

Hashing is a useful and inexpensive way to obfuscate, index, or group results into convenient subdivisions. HashCode is a common and simple algorithm used by Java across many platforms that can be translated into, and used in TSQL if desired. This allows us to guarantee identical results between TSQL scripts and application code.

Attached to this article is the full script that we built above. Feel free to download, reuse, and customize this script as needed. While very iterative in its approach, the fact that we are operating on scalar variables allows this to perform well, even if we decide to parse longer lists of larger strings. Extremely long lists might perform a bit slower, but generally will be acceptable. A test run of 1000 strings with an average of 25 characters completed in under a second, even on slow spinning-disk drive storage.

Enjoy!