In this article, we will describe the relation between the Set Theory and SQL Server Set Operations
Introduction to the Set Theory
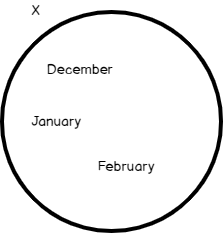
A set is an exactly defined collection of objects. Objects in this collection are called members or elements of the set. The significant point about the set is that the members should be defined exactly and clearly. Definitions whose members are not defined explicitly, it does not identify a set. For example, months of the winter season specifies a set, but some months of the year do not specify a set. Sets are frequently named with capital letters. The members of the sets can be written between the curly braces and separated by the commas. This representation type called Tabular or Roster Form. In the following, the X set represents months of the winter season:
X = {December, January, February}
Also, the sets can be represented by the Venn diagrams:
Universal and Empty set concept in the Set Theory
The sets should provide two essential properties:
- A set member can exist once in a set
- The order of the members of the set is not important
The Universal set is a particular type of the set and the theory assumes that Universal set covers all sets members in the universe and it represented the U letter. On the other hand, if a set does not contain any member, this type of set is named as an Empty set and it is denoted by ∅ or { } sign.
When we apply four operations to the numbers, we are able to obtain new numbers. In a similar context, we can apply some manipulations on sets. In the next sections, we will learn the essential ones and we will also explore the similarities to the SQL Server Set Operations.
Union of sets
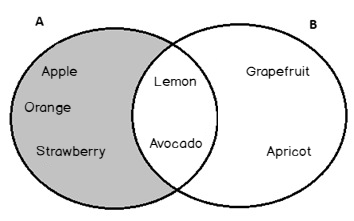
According to the Set Theory, we can union two sets so that we can obtain a new set that contains all members of the unioned sets. In the below example, we will define A and B sets and the members of these sets will be fruits:
A = {Apple, Orange, Strawbery, Lemon, Avocado}
B = {Lemon, Avocado, Grapefruit, Apricot}
The union of the A and B sets will look as follow and it is denoted by A U B:
A U B = {Apple, Orange, Strawbery, Lemon, Avocado, Grapefruit, Apricot}
The following Venn diagram illustrates A union B:
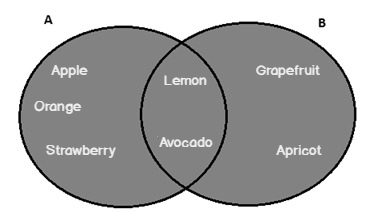
At this point, we must emphasize one issue, the common set members are shown only once.
In the SQL Server, the UNION operator concatenates the resultsets of the two tables and it eliminates the duplicated rows from the resultset. In fact, the UNION operator in SQL Server acts as like as the union operation in the Set Theory. Suppose that, A and B sets are represented by tables in SQL Server. At first, we will create these tables and then add the expressions that similar to A and B set members:
|
1 2 3 4 |
CREATE TABLE TABLE_A (FruitName VARCHAR(100)) INSERT INTO TABLE_A VALUES ('Apple'),('Orange'),('Strawbery'),('Lemon'),('Avocado') CREATE TABLE TABLE_B (FruitName VARCHAR(100)) INSERT INTO TABLE_B VALUES ('Lemon'),('Avocado'),('Grapefruit'),('Apricot') |
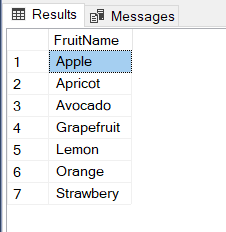
When we union these tables the resultset will be similar to A union B result:
|
1 2 3 |
SELECT * FROM TABLE_A UNION SELECT * FROM TABLE_B |
When we change the order of the tables in the query, the result set will not change:
|
1 2 3 |
SELECT * FROM TABLE_B UNION SELECT * FROM TABLE_A |
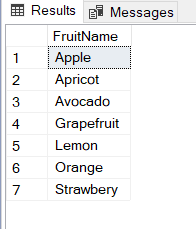
The Intersection of sets
The intersection of the two sets generates a set that contains the common members of the intersected sets. Now, we will observe the intersection of the A and B sets. The A intersection B is denoted by A ∩ B:
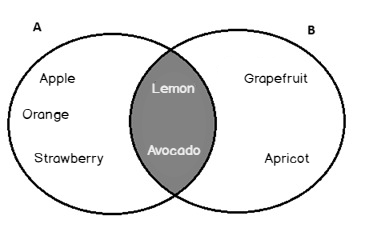
A ∩ B = {Lemon, Avocado}
The result will be Lemon and Avocado; these two members are common members for the A and B sets:
A ∩ B is equal to B ∩ A:
B ∩ A = {Lemon, Avocado}
The yellow shaded area illustrates the intersection of the A and B sets in the Venn diagram:
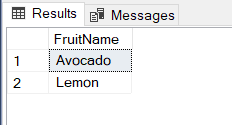
In SQL Server, the INTERSECT operator implements the intersection logic of the Set Theory to tables. Now, we will find the intersection of the TABLE_A and TABLE_B with help of the following query:
|
1 2 3 |
SELECT * FROM TABLE_A INTERSECT SELECT * FROM TABLE_B |
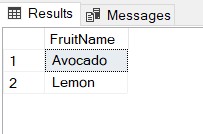
The resultset will not change when we change the order of the tables:
|
1 2 3 |
SELECT * FROM TABLE_B INTERSECT SELECT * FROM TABLE_A |
Difference of sets
The members that are in a set and are not exist in the other are called a set difference in the Set Theory. The result of the A difference B set will be as follows and it is denoted A / B:
A \ B = {Apple, Orange, Strawberry}
The blue shaded area illustrates the result of the A difference B set in the Venn diagram:
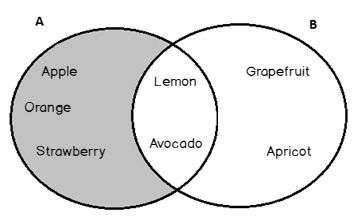
A / B is not equal to B / A
B / A = {Graperfruit , Apricot }
The purple shaded area illustrates B difference A in the Venn diagram:
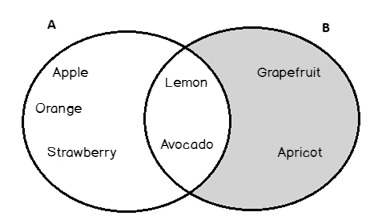
In SQL Server, with the help of the EXCEPT operator, we can obtain the difference between the two tables:
|
1 2 3 |
SELECT * FROM TABLE_A EXCEPT SELECT * FROM TABLE_B |
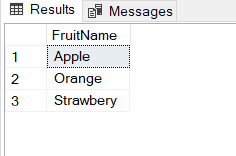
When we change the order of the table, the result set will be changed:
|
1 2 3 |
SELECT * FROM TABLE_B EXCEPT SELECT * FROM TABLE_A |
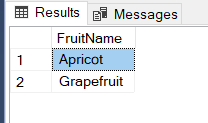
Conclusion
In this article, while the Set Theory is an abstract concept, we have seen it became a concrete reality in relational database theory.
“Without mathematics, there’s nothing you can do. Everything around you is mathematics. Everything around you is numbers” – Shakuntala Devi
Most of his career has been focused on SQL Server Database Administration and Development. His current interests are in database administration and Business Intelligence. You can find him on LinkedIn.
View all posts by Esat Erkec
- SQL Performance Tuning tips for newbies - April 15, 2024
- SQL Unit Testing reference guide for beginners - August 11, 2023
- SQL Cheat Sheet for Newbies - February 21, 2023