From mathematics to SQL Server, a fast introduction to set theory

Introduction

In the previous article of this series “An introduction to set-based vs procedural programming approaches in T-SQL”, we’ve seen from a simple example that we could find actual benefit from learning set-based approach when writing T-SQL code.

In this article, we will carry on in this way by having a look at what a set is and what we can do with it in a mathematical point of view and how it’s implemented and provided to us in SQL Server. We will also have a look at more “realistic” examples using Microsoft’s AdventureWorks database.

Set Theory and fundamentals

Set definition

In mathematics, we define set theory is a branch of mathematics and more particularly mathematical logic that studies collections of objects we refer to as sets.

Don’t worry, we won’t do a lot of maths here as we will focus on practical aspects that we will use when writing T-SQL queries. Let’s just review some fundamentals of this theory:

The elementary set is the empty set. It’s a collection of zero objects and you will find in some references, it’s also called the null set. Its notation is ∅ or { }.
A non-empty set contains the empty set plus one or more objects. This also means that a set can contain a set.
There is a fundamental binary relation between an object and a set: object to set membership. This is equivalent to the IN operation in a T-SQL query.
As a set can contain another set, last binary relation can be extended to set to set membership also known as subset relation or set inclusion.
Just like any arithmetic theory, set theory defines its own binary operations on sets. As an example, in number theory, we can find operations like addition or division.

Graphical representation of a set

In order to graphically represent an operation on sets, it’s common to use Venn diagrams, which show all possible logical relations between a finite number of different sets.

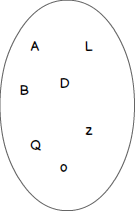
You will find an example of representation for a single set and its objects in following figure. This set contains the following objects: A, B, D, L, o, Q and z.

In following, we will use this representation in order to provide a good understanding of the product of each operation we will define.

Set operations and their equivalent in SQL Server

Now, let’s talk about operations on two sets called A and B. We will also translate them to T-SQL statements where A and B will be either tables or the results of a query.

As almost all readers should know, the way to get the content of either set A or set B is performed as followed using T-SQL (example with set A):

SELECT *

FROM A

Note

In following, except where otherwise stipulated, T-SQL « sets » A and B have the same number of columns of same types. This is the reason why we used SELECT * notation above.

The union operation

The union operation will produce set made up with all the objects from A and all objects from B. It’s denoted as A∪B.

For instance, if A is composed of {1,3,6} and B of {3,9,10} then A∪B is a set composed of {1,3,6,9,10}.

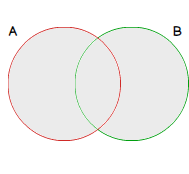
Graphical representation of A∪B is as follows. Set A is represented by red circle while green circle represents Set B. A∪B is the grayscaled parts of those circles. Further representations will use this color usage convention.

In SQL Server, we will find an implementation of the UNION operator. You will find below an equivalent T-SQL statement to the A∪B set:

SELECT *

FROM A

UNION

SELECT *

FROM B

There is a little difference between T-SQL and set theory: Microsoft provides the possibility for their user to keep duplicate records that should normally be erased by UNION operator. To do so, we will append the word ALL after UNION.

Back to the previous example using sets of numbers, the UNION ALL of set A with set B will generate following set:

{1,3,3,6,9,10}

Now, let’s take an example using SQL Server and check that there is an actual difference between UNION and UNION ALL operators.

Union Example

Union all Example

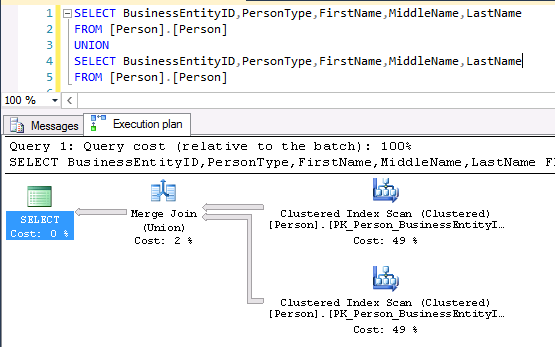
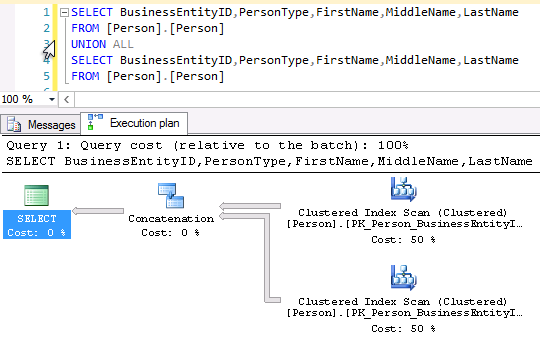
As we can see in the above example, UNION operation is translated to MERGE JOIN operator in SQL Server while UNION ALL operator simply takes up all rows from each set and concatenates it.

So far, we haven’t seen what a « join » is. Basically, a join is a way to get a set based on two or more tables. This results set has either the same columns as base tables or column from both tables implied in join operation.

The intersection operation

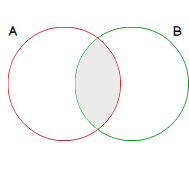
The intersection of set A and set B is denoted A∩B and is the set of elements that can be found in both sets.

Back to the example with numeric sets,

A = {1,3,6}
B = {3,9,10}
A∩B = {3}

Graphically, it looks like:

In SQL Server, there is also an INTERSECT T-SQL operator that implements this set operation. You will find below an equivalent T-SQL statement to the A∪B set:

SELECT *

FROM A

INTERSECT

SELECT *

FROM B

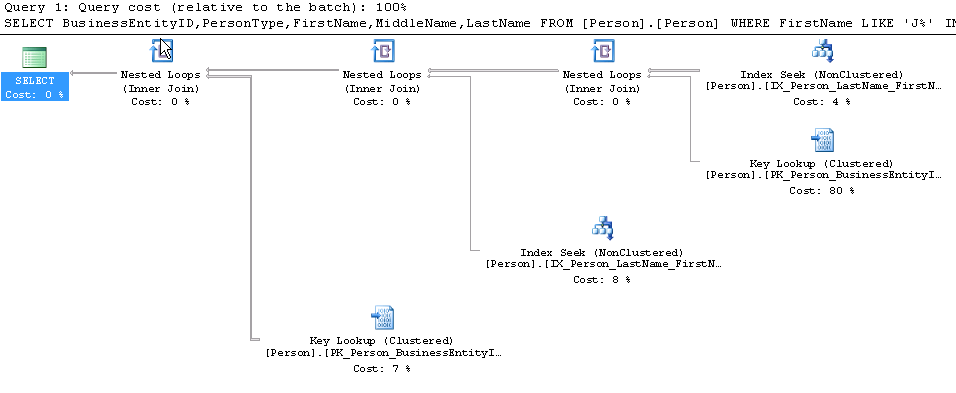
Now, let’s look at a concrete T-SQL example where A is the set of persons with firstname starting with a « J » and B is the set of persons with lastname starting with a « E ». A∩B is the set of persons with « J. E. » as initials.

SELECT BusinessEntityID,PersonType,FirstName,MiddleName,LastName

FROM [Person].[Person]

WHERE FirstName LIKE 'J%'

INTERSECT

SELECT BusinessEntityID,PersonType,FirstName,MiddleName,LastName

FROM [Person].[Person]

WHERE LastName LIKE 'E%'

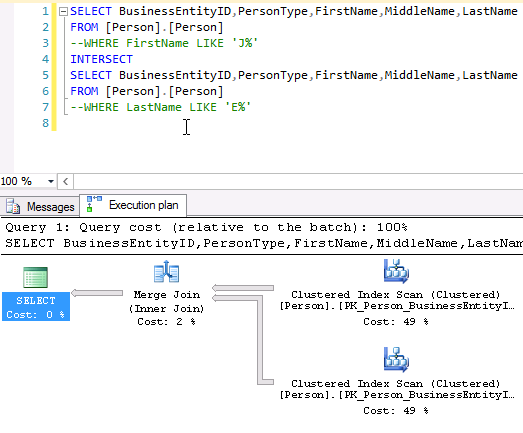
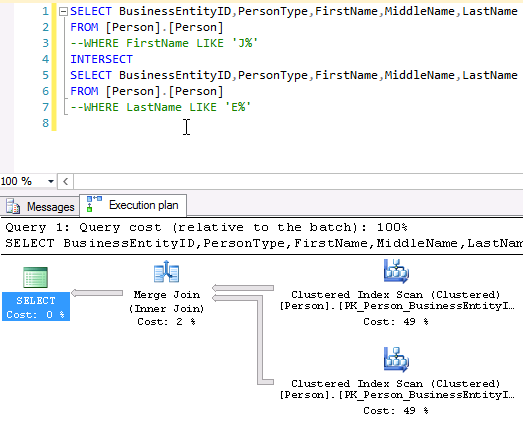
The execution plan for this particular query does not represent the equivalent operator in SQL Server database engine. As we can see, the INTERSECT operation is translated into a chain of Nested Loop operators as we have a WHERE clause in each sub-query.

If we comment those WHERE clauses, we will get following execution plan, that uses a MERGE JOIN operator, like for the UNION operation but in an « inner join » mode:

Set difference operation

The difference between a set A and a set B is denoted A \ B and will take all the elements composing set A that are not in set B.

Back to the example with numeric sets,

A = {1,3,6}
B = {3,9,10}
A \ B = {1,6}

Graphically, it looks like:

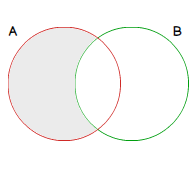
In SQL Server, this operation is also implemented and available to users via EXCEPT operator. You will find below an equivalent T-SQL statement to the A \ B set:

SELECT *

FROM A

EXCEPT

SELECT *

FROM B

So, if we want to get a concrete example, let’s say we want to get the identifier of all persons that do not have a contact phone number. To do this, we will take table Person.Person as set A and Person.PersonPhone table as set B. This gives us following statement:

SELECT BusinessEntityID

FROM [Person].[Person]

EXCEPT

select BusinessEntityID

from Person.PersonPhone

If we take a look at its execution plan, we see that the operator used by SQL Server is called « Hash Match (Left Anti Semi Join) ».

The Cartesian product operation

Operation explanation

The Cartesian product is denoted A × B and is the set made up with all possible ordered pairs (a,b) where a is member of set A and b is member of set B.

Back to our example using numbers where:

A = {1,3,6}
B = {3,9,10}

In order to get the elements of A × B, we can make a table with an element of A by row and an element of B by column. Each combination of row and column values will be an element of A × B.

	Elements of set B
Elements of set A	3	9	10
1	(1,3)	(1,9)	(1,10)
3	(3,3)	(3,9)	(3,10)
6	(6,3)	(6,9)	(6,10)

So, A × B = {(1,3),(1,9),(1,10),(3,3),(3,9),(3,10),(6,3),(6,9),(6,10)}

Well, we might be very confused when seeing this operation and be asking ourselves « what the hell can I do with that? ». Actually, this operation is very useful in a wealth of situations and we will use it extensively in last article of this series.

We will first have a look at the way to run a cross join using T-SQL.

Corresponding implementation in SQL Server

In SQL Server, we can write a Cartesian product using CROSS JOIN command as follows.

SELECT *

FROM A

CROSS JOIN B

Note:

Here, star will return all columns from A and from B
If we would like to cross join A with itself, we would get following error message except if we provide an alias for at least one of table A occurrences.

Alternatively, we can simply use a comma to replace CROSS JOIN notation:

SELECT *

FROM A, B

Cross join real life application example usages

Now we know how to write a query using a cross join or Cartesian product, well, we should know in which cases we could use it.

Example 1: Compute/Generate all possible cases for a particular situation

Let’s assume we are in a clothing factory and we want to know how many different kinds of pieces we can create and at which cost, based on clothing size and clothing color.

If we have a ClothingSizes and a ClothingColors tables, then we can take advantage of CROSS JOIN operation as follows.

-- Create ClothingSizes table

CREATE TABLE ClothingSizes (

SizeDisplay VARCHAR(32),

Need4FabricUnits INT

);

INSERT INTO ClothingSizes

VALUES

('Small',1), ('Medium',2),('Large',3),('Extra Large',4)

;

-- Create ClothingColors table

CREATE TABLE ClothingColors (

ColorName VARCHAR(32),

ColorPrice INT

);

-- Generate all combinations

INSERT INTO ClothingColors

VALUES

('White',10),

('Gray',12),

('Red',15),

('Yellow',20),

('Black',10)

;

SELECT

cs.SizeDisplay,

cc.ColorName,

cc.ColorPrice * cs.Need4FabricUnits as ManufactoringPrice

FROM ClothingSizes cs,

ClothingColors cc

-- cleanups

DROP TABLE ClothingColors;

DROP TABLE ClothingSizes;

The results:

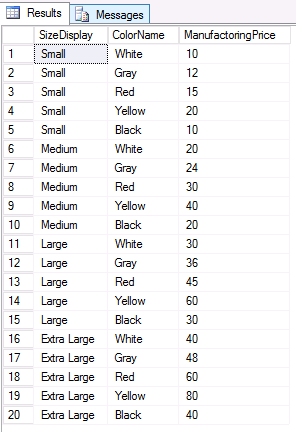
Example 2: Generate test data

With the example above, you can imagine a solution with a list of first names and a list of last names. When performing a cross join on both, we would get candidates for a Contact or a Person table. This can also be extended to addresses and any kinds of data. Your imagination is the limit.

Example 3: Generate charts data (X axis)

This example is part of an advanced example for set-based approach so it won’t be developed in details here. We will just present the situation. Let’s say we have a tool that logs any abnormal behavior with timestamp inside a SQL Server table but does not log anything when everything works like expected. In such a case, if we want, for instance, to plot number of abnormalities occurrences by day, we will face a problem as there are « holes » in data.

So, we cannot plot a chart directly and we have to first generate a timeline with the appropriate step (here hours). To generate this timeline, we would need to use CROSS JOIN.

In summary, we would consider a set containing short dates of interest, then cross join them with a collection of 24 numbers from 0 to 23, representing hours in a day.

If we would need to report by minutes in a day, we would add another CROSS JOIN operation with a collection of 60 numbers from 0 to 59 representing minutes in an hour.

Mathematical operations with no equivalent in SQL Server

These set operations are not that easy to implement so that it will work for every single case in an efficient manner. I think that’s the reason why Microsoft did not implement them.

In following, we will present the operation itself, an example use case where they could be useful and an implementation specific to this use case.

The symmetric difference operation

Symmetric difference operation is equivalent to a logical XOR. It’s denoted as A⊕B and contains all the elements that are in set A but not in set B and those that are in set B but not in set A.

Graphically, this operation can be represented as:

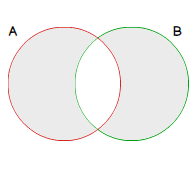
We can implement it in different ways:

Implementation 1 – simply like its definition

(

SELECT *

FROM A

EXCEPT

SELECT *

FROM B

) UNION ALL (

SELECT *

FROM B

EXCEPT

SELECT *

FROM B

)

Implementation 2 – Using IN operator for key columns

SELECT *

FROM A

WHERE A_Keys NOT IN ( SELECT B_Keys FROM B)

UNION ALL

SELECT *

FROM B

WHERE B_Keys NOT IN (SELECT A_Keys FROM A)

The power set operation

Power set of a set A is the set composed of all possible subsets of set A.

In our former example using sets of numbers, A = {1,3,6}. This means that the power set of A is composed of following elements:

The empty set
Sets of one element {1}{3}{6}
Sets of two elements {1,3}{1,6}{3,6}
Sets of three elements (which is actually set A).

I haven’t found any particular reason to use this set operation in real life, but feel free to contact me if you find one!

Summary

In this article, we’ve seen that SQL Server implements most of mathematical operations on sets. We can add the set operators defined here on the right of the table create in previous article of this series –“An introduction to set-based vs procedural programming approaches in T-SQL”. As a reminder, this table summarizes instructions and objects we can use in both procedural and set-based approaches.

Procedural Approach	Set-Based Approach
SELECT and other DML operations, WHILE, BREAK, CONTINUE, IF…ELSE, TRY…CATCH Cursors (OPEN, FETCH, CLOSE) DECLARE	SELECT and other DML operations, Aggregate functions (MIN, MAX, AVG, SUM…) UNION and UNION ALL EXCEPT and INTERSECT CROSS JOIN

SQLShack

From mathematics to SQL Server, a fast introduction to set theory

Introduction

Set Theory and fundamentals

Set operations and their equivalent in SQL Server

Summary

Further readings

Introduction

Set Theory and fundamentals

Set operations and their equivalent in SQL Server

Summary

Further readings

Related posts: